We provide cutting edge point-of care diagnostic technologies.
Platforms that can run multiple immunofluorescence chromatography assays – including for active COVID-19 infection and IgG / IgM. Fully CE-marked for use EU-wide.
COVID-19 test is approved by the MHRA under the Coronavirus Test Device Approvals legislation (CTDA).
How do we measure accuracy?
Most manufacturers brag about sensitivity and specificity.
But that’s not the whole picture. Those are of little use if a test only identifies people with the highest levels of virus.
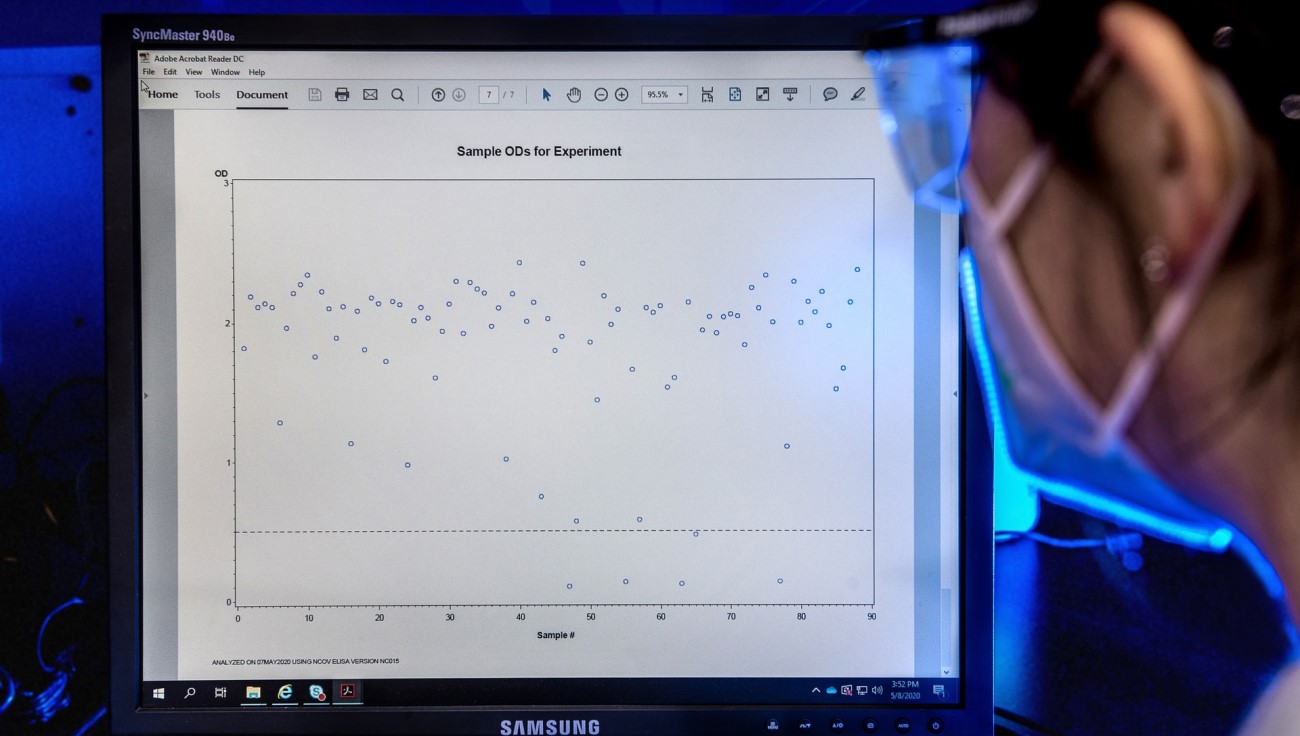
Sensitivity by PCR Ct
A low Ct value on PCR indicates a lot of viral RNA is in the sample. It’s generally considered that people with a Ct value over 30 don’t present a significant infection risk1, 2, 3, 4, 5, 6 and presence of viral RNA may well be from a past infection. You can see from the graph above how closely the MFX test correlates with positivity on PCR in those most likely to be infectious.
The Ct30 threshold is based on a combination of of antigen sensitivity and studies of virus culture by Ct, where the presence of culturable virus is assumed to correlate with infectivity7.
Figures above independently verified in clinical samples by the Hampshire Hospitals NHS Foundation Trust
Sensitivity is the ability of a test to correctly identify patients with a disease.
Specificity is the ability of a test to correctly identify patients without the disease.
How much virus needs to be in the sample for a reliably positive result.
A game-changing innovation in COVID-19 testing.
A game-changing innovation in COVID-19 testing.
Only diagnoses active infections: no false positives due to past infections – unlike PCR and LAMP

Paul Matthews
Paul has more than twenty years’ experience in various commercial roles. His background includes senior positions in Forex, marketing, aviation, and business management.

Simon Lane
Simon has a wealth of board experience in an eclectic mix of industries from biotech to precious metals to FMCG. Simon leads the MFX client exerience team and relishes the complex challenges that COVID-19 testing presents.
Contact Us
Please get in touch and one of our team will be in contact. No pushy salesmen – promise – we just let the science do the talking.